Posts tagged "privacy":
Privacidad Diferencial: introducción
→ [pdf] ←Privacidad diferencial (differential privacy) es un termino que posiblemente habrás visto asociado a la privacidad de datos o información. En los últimos años ha tomado mucha relevancia, primero en el mundo académico y posteriormente a nivel comercial gracias a que grandes empresas como Google[1] o Apple[2] anunciaron el uso de privacidad diferencial para proteger los datos de sus usuarios. Pero ¿qué es la privacidad diferencial? ¿Como nos garantiza la privacidad o anonimato de datos de usuarios? ¿Es realmente efectiva?
1. Consultando una base de datos
Vamos a suponer que tenemos una base de datos que llamaremos \(D\) con información sobre ciertos usuarios. Esta base de datos contiene información confidencial sobre los usuarios como pueden ser datos personales o fiscales. Como ejemplo y de forma muy simplificada, supongamos que la base de datos contiene los siguientes registros (entendemos por registro cada fila):
| nombre | edad | salario |
|---|---|---|
| Ataúlfo | 43 | 100 |
| Sigerico | 15 | 300 |
| Walia | 50 | 200 |
| Teodoredo | 51 | 100 |
| Turismundo | 16 | 500 |
| Tedorico II | 40 | 300 |
| Eurico | 14 | 700 |
| Alarico II | 49 | 300 |
| Gesaleico | 69 | 500 |
| Amalarico | 17 | 200 |
Para obtener información de la base de datos permitimos que otros usuarios hagan consultas y obtengan las correspondientes respuestas.
Por ejemplo, supongamos que queremos permitir que se pueda obtener la consulta: "número de registros/individuos mayores de edad". Es decir, el número de individuos con edad igual o superior a 18. Denotaremos esta consulta como la función \(f\), y el resultado de aplicar la consulta a la base de datos \(D\), como \(f(D)\).
\(f(D)\) \(=\) núm. de usuarios en \(D\) con edad \(\geq\) 18
Si hacemos la consulta a la base de datos \(D\) anterior obtendremos que \(f(D)=6\).
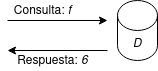
Podríamos pensar que esta consulta \(f\) es segura, ya que no obtenemos información sensible de ningún usuario en concreto. Obtenemos información agregada, que no nos esta revelando datos específicos de ningún usuario. Sin embargo y como veremos, esta consulta aparentemente inocente puede acarrear problemas de privacidad y revelar información sensible sobre los usuarios de la base de datos.
2. ¿Que pasa si tenemos versiones diferentes de la base de datos?
Supongamos que tenemos dos versiones diferentes de la base de datos anterior que denotamos como \(D_1\) y \(D_2\). Estas dos bases de datos son idénticas a excepción de un solo registro. Por ejemplo:
| nombre | edad | salario |
|---|---|---|
| Ataúlfo | 43 | 100 |
| Sigerico | 15 | 300 |
| Walia | 50 | 200 |
| Teodoredo | 51 | 100 |
| Turismundo | 16 | 500 |
| Tedorico II | 40 | 300 |
| Eurico | 14 | 700 |
| Alarico II | 49 | 300 |
| Gesaleico | 69 | 500 |
| Amalarico | 17 | 200 |
| nombre | edad | salario |
|---|---|---|
| Ataúlfo | 43 | 100 |
| Walia | 50 | 200 |
| Teodoredo | 51 | 100 |
| Turismundo | 16 | 500 |
| Tedorico II | 40 | 300 |
| Eurico | 14 | 700 |
| Alarico II | 49 | 300 |
| Gesaleico | 69 | 500 |
| Amalarico | 17 | 200 |
En este caso, \(D_2\) es igual a \(D_1\) con la excepción de que le falta un registro, el correspondiente a Sigerico.
Cuando la diferencia entre dos bases de datos \(D_1\) y \(D_2\) es de un solo registro, lo denotamos como \(d(D_1, D_2) = 1\).
¿Que pasa si hacemos la consulta anterior en \(D_1\) y \(D_2\)?
- \(f(D_1) = 6\)
- \(f(D_2) = 6\)
¿Hay ahora algún problema de privacidad? El lector avispado tenderá a pensar que sí (¿porqué si no estamos haciendo todo esto?).
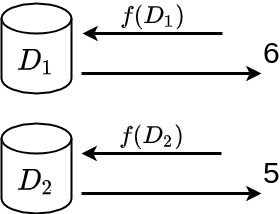
Supongamos que quien hace las dos consultas (en adelante el atacante) sabe que \(D_2\) tiene un registro menos que \(D_1\). Puede incluso saber que dicho registro corresponde a un usuario concreto, ya que este ha solicitado borrar su información de la base de datos. Al no conocer los registros de la base de datos, el atacante no sabe la edad ni el salario de dicho usuario, pero ahora sí sabe que no es mayor de edad. Es decir, ha obtenido información nueva que no tenia sobre un usuario concreto de la base de datos.
3. Entra en juego la privacidad diferencial
La privacidad diferencial proporciona una definición de privacidad que se basa en controlar la información que se filtra en el ejemplo anterior. De manera muy zafia podemos decir que:
Una consulta a una base de datos, como nuestra consulta \(f\), cumple privacidad diferencial si al hacer la misma consulta en \(D_1\) y \(D_2\) no obtenemos mucha información nueva.
Es decir, si el atacante hace la consulta a las dos bases de datos, no se revela mucha más información de la que ya tenia. O dicha información esta acotada. Aquí hay varios puntos a destacar:
- ¿Qué queremos decir con que se revele mucha o poca información? Este es un punto clave y difícil de precisar que de momento no abordaremos de forma directa. Veremos más adelante como se mide o acota esta información en privacidad diferencial.
- Esto se tiene que cumplir para cualquier par de versiones de la base de datos que difieran en un solo registro (sea cual sea ese registro). Es decir, cualquier \(D_i\) y \(D_j\) tal que \(d(D_i, D_j) = 1\).
- Hablamos de que la información que se obtiene está acotada y no de que no se obtiene ninguna información. Esto último seria ideal desde el punto de vista de la privacidad, pero si fuese así, la consulta \(f\) tendría que, por ejemplo, retornar un valor constante independientemente del registro que falte. Cosa que no resultaría nada útil (no serviría de nada realizar dicha consulta).
¿Como podemos conseguir esto? La manera más inmediata es intentar sustituir nuestra consulta \(f\) por otra versión más segura que llamaremos \(K_f\). Esta nueva función debe cumplir con dos requisitos importantes:
- Debe ser útil. Quien hace la consulta quiere obtener información sobre el numero de registros con personas mayores de edad. Esto tiene que seguir siendo así en la medida de lo posible. No podemos retornar un valor constante o muy alejado del real.
- Deber ser segura o conseguir un nivel de privacidad aceptable. La información que un atacante pueda obtener haciendo la consulta a diferentes versiones de la base de datos tienes que ser muy poca.
¿Como podemos implementar \(K_f\)?
4. Privacidad diferencial con ruido
La manera más sencilla de pensar en esta función segura \(K_f\) es considerarla como la función original pero con cierto ruido añadido: \(K_f(D) = f(D) + r\), donde \(r\) es un valor de ruido elegido al azar. Es decir, cuando hacemos la consulta \(f\) obtendremos el número de personas mayores de edad con un ruido o error añadido.
¿Porque es esto interesante?
- El resultado puede ser útil en la medida en que el ruido sea relativamente pequeño. Al hacer la consulta, no obtenemos el número exacto de personas mayores de edad, pero sí que obtenemos una aproximación que en muchos casos puede ser suficiente.
- Se consigue un cierto nivel de privacidad debido a la incertidumbre que hay ahora sobre el resultado. Cuando el atacante hace dos consultas en dos versiones de la base de datos la diferencia entre los valores que obtiene puede venir determinada por el ruido de las dos consultas y no necesariamente o directamente por la diferencia que pueda haber entre los valores reales.
Todo esto que planteamos de forma un poco confusa, se concreta en la conocida definición de privacidad diferencial, que de forma un poco más formal detallamos a continuación.
Una función \(K_f\) para una consulta \(f\), proporciona ε-privacidad diferencial si para todas las bases de datos \(D_1\) y \(D_2\) que difieren en un solo elemento, y para todo \(S \subseteq Rango(K_f)\):
\begin{equation} P[K_f(D_1) \in S] \leq e^\epsilon \cdot P[K_f(D_2) \in S] \end{equation}Pero, ¿que quiere decir todo esto?. Vayamos por partes:
- \(Range(K_f)\): el rango (Range) de una función es el conjunto de todos los valores que puede retornar. Es decir, \(Range(K_f)\) es el conjunto de todos los valores que puede retornar la función \(K_f\). En nuestro caso podriamos considerar que el rango de \(K_f\) es el conjunto de todos los numero enteros iguales o mayores que \(0\) (la función \(f\) no puede retornar un número negativo).
- \(S \subseteq Range(K_f)\): \(S\) es un subconjunto de \(Range(K_f)\). Es decir cualquier subconjunto de numeros enteros mayores o iguales a \(0\). Algun ejemplo podria ser \(S=\{0,1,2,3,4,5\}\), \(S=\{3,5,11\}\), \(S=\{100, 235, 24\}\), …
- \(P[K_f(D_1) \in S]\): se refiere a la probabilidad de que el resultado de aplicar \(K_f\) a \(D_1\) pertenezca al subconjunto \(S\).
Estamos mirando entonces la diferencia que hay entre la probabilidad de que la consulta a \(D_1\) y \(D_2\) pertenezca al mismo subconjunto \(S\), sea cual sea \(S \subseteq Range(K_f)\). O dicho de otra manera, que la diferencia entre la consulta \(K_f(D_1)\) y \(K_f(D_2)\) sea lo menos perceptible posible. Donde este menos perceptible posible queda acotado de forma más precisa diciendo que tiene que ser menor que \(e^\epsilon\).
Si la función \(K_f\) cumple la condición anterior decimos que cumple privacidad diferencial para \(\epsilon\), o que cumple \(\epsilon\) -differential privacy.
Esta condición a veces se expresa en forma de conciente:
\begin{equation} \frac{P[K_f(D_1) \in S]}{P[K_f(D_2) \in S]} \leq e^\epsilon \end{equation}Por ejemplo, supongamos que definimos el ruido \(r\) como un valor elegido de forma aleatoria y uniforme del conjunto de números \(\{-2, -1, 0, 1, 2\}\). Siguiendo con el ejmplo de la función \(K_f\), supongamos que hacemos la consulta a \(D_1\) y \(D_2\) y en cada caso obtenemos los valores de ruido \(r_1=-1\), \(r_2=0\). Es decir:
- \(K_f(D_1) = 6 + r_1 = 6 - 1 = 5\)
- \(K_f(D_2) = 6 + r_2 = 6 + 0 = 6\)
Es importante remarcar que los valores \(r_1\) y \(r_2\) los elije la BD y obviamente se mantienen en secreto. Quien recibe el resultado de la función \(K_f\) desconoce el ruido que ha sido sumado.
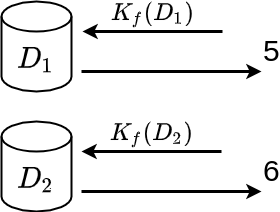
Ahora existe diferencia entre las dos respuestas pero resulta más difícil poder obtener información sobre el valor del registro que ha sido eliminado en \(D_2\). No podemos saber con certeza si corresponde a una persona mayor o menor de edad, ya que no sabemos el ruido que ha sido añadido en cada caso.
Sí que sabemos que dicho ruido puede ser un valor del conjunto \(\{-2, -1, 0, 1, 2\}\). Como cada uno de estos valores tiene la misma probabilidad de ser elejido por la función \(K_f\), podemos intentar ver cual seria el valor original.
En el caso de \(D_1\) tenemos que \(K_f(D_1) = 5\), y sabemos que \(K_f(D_1) = f(D_1) + r_1\). El atacante, no conoce el valor \(f(D_1)\), ni \(r_1\). ¿Puede llegar a saber el valor de \(f(D_1)\)? Inicialmente no, pero puede hacer una estimación. Dependiendo del ruido que se haya utilizado tendremos los valores que se muestran en al siguiente tabla:
| r1 | \(f(D_1)\) |
|---|---|
| -2 | 7 |
| -1 | 6 |
| 0 | 5 |
| +1 | 4 |
| +2 | 3 |
Es decir, los posibles valores de \(f(D_1)\) son \(\{7, 6, 5, 4, 3\}\). De la misma manera, los posibles valores de \(f(D_2)\) serian \(\{8, 7, 6, 5, 4\}\).
A modo ilustrativo, podemos ver en la siguiente tabla la probabilidad de que \(K_f(D_1)\) o \(K_f(D_2)\) pertenzca a algun conjunto \(S\) de ejemplo.
| S | \(P[K_f(D_1) \in S]\) | \(P[K_f(D_2) \in S]\) |
|---|---|---|
| \(\{3\}\) | \(1/5\) | \(0\) |
| \(\{6, 5, 4\}\) | \(3/5\) | \(3/5\) |
| \(\{8, 7\}\) | \(2/5\) | \(1/5\) |
Podemos decir p.e. que nuestra función \(K_f\) no satisface privacidad diferencial para \(\epsilon = 1\). Para mostrarlo, podemos dar un contraejemplo ya que es fácil ver que no se cumple la siguiente condición: \[ P[K_f(D_1) \in \{3\}] \leq e P[K_f(D_2) \in \{3\}] \]
Como veremos más adelante, en privacidad diferencial se utilizan valores de ruido obtenidos a partir de distribuciones de probabilidades concretas. Siendo la más popular la distribución de Laplace.
En la terminología de privacidad diferencial se utilizan los siguiente términos:
- mechanism (mecanismo)
- función o algoritmo que recibe una base de datos como parámetro y retorna un resultado. En nuestro caso seria la función \(f\).
- randomized mechanism (mecanismo aleatorio)
- mecanismo al que se añade aleatoriedad con el fin de proporcionar privacidad a la respuesta. En nuestro caso, la función \(K_f\).
5. La privacidad o revelación de información es acumulativa
La privacidad diferencial permite establecer de manera precisa la noción de acumulación de privacidad o, como se suele decir, presupuesto de privacidad (privacy budget). La idea es que la propiedad de privacidad diferencial se puede ver como un presupuesto de privacidad que se va gastado cada vez que se usa.
Por ejemplo, tomamos el mecanismo aleatorio anterior \(K_f\) que retorna la media de edad mas un ruido elegido de forma uniforme entre el conjunto \(\{-2, -1, 0, 1, 2\}\).
Dada una base de datos \(D_1\) como la anterior podemos obtener el resultado \(K_f(D_1) = 5\). Con este resultado un atacante no sabe el valor original \(f(D_1)\) (que recordamos es 6), pero puede saber que será un número del conjunto \(\{7, 6, 5, 4, 3\}\). La probabilidad de adivinar el valor original es entonces de \(1/5\).
Pero ¿que pasa, si ahora volvemos a repetir la misma consulta con la misma base de datos? Al repetirla podriamos obtener, por ejemplo, que \(K_f(D_1) = 7\) de donde el atacante aprende que los posibles valores de \(f(D_1)\) en este caso serian \(\{9,8,7,6, 5\}\). En la tabla siguiente vemos lo que aprende el atacante en cada caso:
| Consulta | \(K_f(D_1)\) | ¿ \(f(D_1)\) ? |
|---|---|---|
| 1 | \(5\) | \(7,6,5,4,3\) |
| 2 | \(7\) | \(9,8,7,6,5\) |
El avispado atacante, una vez realiza las dos consultas, puede concluir que el valor que busca (\(f(D_1)\)) estará en el conjunto de posibles valores de las dos consultas. Es decir, es su intersección: \(\{7,6,5\}\). Como vemos, ahora el atacante tiene una probabilidad de \(1/3\) de adivinar el valor \(f(D_1)\). Es decir ha reducido la incertidumbre respecto al valor \(f(D_1)\) y por tanto se ha reducido la privacidad que conseguimos con la función \(K_f\).
Si un atacante puede realizar la misma consulta varias veces a la misma base de datos, la incertidumbre que proporciona el mecanismo aleatorio se reduce. En general, cuantas más veces pueda repetir la consulta, mayor certeza tendrá sobre el valor original y mayor será la probabilidad de acierto.
Este ejemplo ilustra la idea de presupuesto de privacidad que se va gastando (o reduciendo) cada vez que se hace una consulta. Tendremos entonces que imponer restricciones o límites en el numero de consultas que se pueden hacer. Estas restricciones quedan formuladas en privacidad diferencial con lo que se conoce como teorema de composición.
6. Continuará…
¿Cómo podemos diseñar mecanismos más realistas? ¿Cómo se calcula \(\epsilon\) en el caso general? ¿Cómo establecemos el presupuesto de privacidad y cómo lo calculamos?
7. References
El mecanismo de Laplace
→ [pdf] ←Sabemos que una manera de proporcionar privacidad diferencial es mediante el uso de un mecanismo aleatorio que puede consistir en añadir ruido a una consulta (o mecanismo) que se realiza a la base de datos.
Ahora veremos un ejemplo de mecanismo aleatorio basado en esta idea conocido como el mecanismo de Laplace. Se trata de uno de los mecanismo más estudiados y sencillos utilizados en privacidad diferencial.
Para introducir este mecanismo veremos que es la sensibilidad de una función, un concepto importante en privacidad diferencial. Esto nos permitirá determinar, en cierta manera, la cantidad de ruido que tenemos que añadir para conseguir un nivel de privacidad determinado a una consulta o función.
Vamos a repasar también, aunque de forma muy rápida, como es una distribución de Laplace, que nos determinará el ruido generado.
1. Distribución de Laplace
La distribución de Laplace (también conocida como doble exponencial) es una distribución de probabilidades continua. Su función de densidad de probabilidad se expresa como:
\[ f(x | \mu, b) = \frac{1}{2b} \exp\left(-\frac{|x - \mu|}{b}\right)\]
donde \(\mu\) es un parámetro de posición o localización y \(b > 0\) un parámetro de escala (o diversidad). Denotaremos esta distribución como \(Lap(\mu, b)\).
A continuación mostramos la distribución de Laplace \(Lap(0, 1)\), es decir, con \(\mu = 0\) y \(b = 1\).
import scipy.stats import matplotlib.pyplot as plt import numpy as np x = np.linspace(-10,10,1000) dist = scipy.stats.laplace(0, 1) plt.clf() plt.plot(x, dist.pdf(x)) plt.grid() fname = "img/laplace.png" plt.savefig(fname) fname
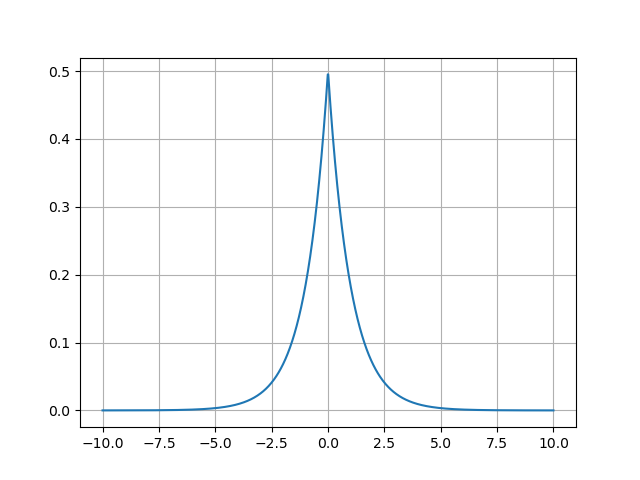
El parámetro \(\mu\) (la media de la distribución) determina la posición o localización de la distribución. Por ejemplo:
plt.clf() for loc in [-3, 0, 3, 6]: dist = scipy.stats.laplace(loc, 1) plt.plot(x, dist.pdf(x), label=f"$\mu = {loc}$") plt.grid() plt.legend() fname = "img/laplace-mu.png" plt.savefig(fname) fname
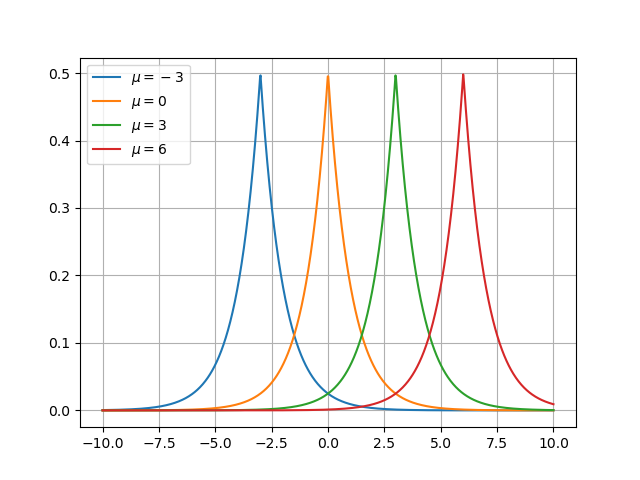
Por otra parte el parámetro \(b\) determina la forma de la distribución (o escala):
plt.clf() for scale in [1, 2, 3, 4]: dist = scipy.stats.laplace(0, scale) plt.plot(x, dist.pdf(x), label=f"$b = {scale}$") plt.grid() plt.legend() fname = "img/laplace-scale.png" plt.savefig(fname) fname
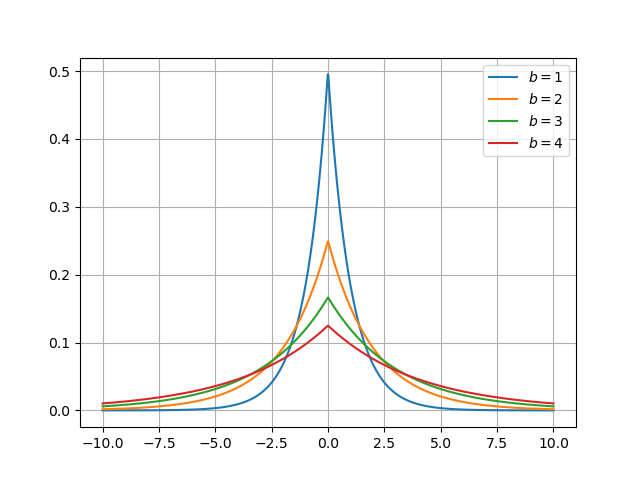
La media de la distribución de Laplace \(Lap(\mu, b)\) es \(\mu\), que coincide con la mediana, y su varianza es \(2b^2\).
2. Sensibilidad global
Consideramos un mecanismo o función \(f\) que realiza una consulta a la base de datos \(D\) generando una respuesta \(f(D)\). Suponemos que los datos a consultar son numéricos y que el resultado puede ser un vector de \(M\) elementos De esta manera, si \(\mathcal{D}\) es el conjunto de todas las posibles bases de datos, \(f: \mathcal{D} \to \mathbb{R}^M\).
La sensibilidad global (global sensitivity) de una funcion \(f\) se suele denotar como \(\Delta f\) o \(GS(f)\), y a veces se llama también \(l_1\) -sensitivity. Queda definida de la siguiente manera:
La sensibilidad global de una función \(f: \mathcal{D} \to \mathbb{R}^M\) es:
\begin{equation} \Delta f = \max_{D_1, D_2 \in \mathcal{D}, d(D_1, D_2) = 1} \lVert f(D_1) - f(D_2) \rVert_{1} \end{equation}En esta definición se utiliza la norma \(l_1\) (\(l_1\) -norm) denotada como \(\lVert \cdot \rVert_1\). Dado un vector \(x \in \mathbb{R}^M\), \(\lVert x \rVert_1 = \sum_{i=1}^M | x_i |\). Podemos ver la norma \(l_1\) simplemente como la suma del valor absoluto de todos los elementos del vector.
Por ejemplo, para el vector \(v = (2, 3, -4, 6)\), su norma \(l_1\) es: \[ \lVert v \rVert_1 = \sum_{i=1}^4 | v_i | = |2| + |3| + |-4| + |6| = 15 \]
La sensibilidad global expresa la máxima diferencia que podemos encontrar al aplicar la función a dos bases de datos que difieren en un solo elemento.
Supongamos que tenemos una base de datos censal con información de la población de nuestra ciudad. Definimos entonces la función \(f_1\) que retorna el número de individuos mayores de edad (con edad mayor o igual a 18).
Tenemos dos versiones de la base de datos que difieren en un solo registro, de manera que, por ejemplo:
\begin{align*} f_1(D_1) = 120\\ f_1(D_2) = 121 \end{align*}en este caso podemos decir que el resultado difiere en 1, pero no es dificil ver que en el caso general la diferencia máxima entre la consulta hecha a dos bases de datos vecinas será 1. Es más, dicha diferencia será siempre -1, 0 ó 1. Podemos entonces decir que la sensivilidad global de \(f_1\) es 1: \[ \Delta f_1 = 1 \]
En general, para cualquier función que consista en contar elementos, como en el ejemplo anterior, tendremos el mismo resultado respecto a su sensivilidad global.
Suponemos ahora que tenemos una segunda funcion \(f_2\) que retorna el número de individuos que han leído el Quijote (información que también incluye la base de datos anterior) y por ejemplo tenemos que:
\begin{align*} f_2(D_1) = 10\\ f_2(D_2) = 10 \end{align*}Al igual que con \(f_1\) es fácil ver que \(\Delta f_2 = 1\).
Vamos ahora a ver la función \(f_c\) que definimos como aquella que retorna un vector con las dos consultas correspondientes a \(f_1\) y \(f_2\), de manera que \(f_c(D) = (f_1(D), f_2(D))\). Siguiendo el ejemplo anterior podríamos tener:
\begin{align*} f_c(D_1) = (120, 10)\\ f_c(D_2) = (121, 10) \end{align*}En este caso la sensibilidad global será de 2. La diferencia máxima para cada función es 1, con lo que la norma \(l_1\) será 2. Es decir \(\Delta f_c = 2\)
El lector obviamente se preguntará que pasa en el caso de funciones más complejas e interesantes. Aquí es donde se puede complicar un poco el asunto ya que podríamos tener funciones para las que su sensibilidad global sea infinito o resulte difícil poder estimar un cálculo. En general necesitaremos que la función este acotada para poder calcular su sensibilidad global. Queda pendiente ver con mayor detalle casos diferentes a funciones que cuenten registros.
3. El mecanismo de Laplace
Llegamos ya a poder ver uno de los mecanismos aleatorios más populares en privacidad diferencial, el conocido como mecanismo de Laplace. Sin muchas sorpresas, éste consiste en añadir ruido siguiendo una distribución de Laplace a la respuesta.
Consideramos una consulta o mecanismo \(f\) que realiza una consulta a la base de datos \(D\) generando una respuesta \(f(D)\). A modo de generalización suponemos que los datos a consultar son numéricos y la respuesta, un vector de \(M\) elementos. De esta manera, si \(\mathcal{D}\) es el conjunto de todas las posibles bases de datos, \(f: \mathcal{D} \to \mathbb{R}^M\).
El mecanismo de Laplace para la función \(f\mathcal{D} \to \mathbb{R}^M\) es:
\begin{equation*} M_L(D, f, \epsilon) = f(D) + (N_1, \ldots, N_M) \end{equation*}donde \(D \in \mathcal{D}\), y \(N_i\) son variables aleatorias independientes que se obtienen a partir de una distribución de Laplace \(N_i \sim Lap(0, \Delta f/\epsilon)\).
Siguiendo el ejemplo anterior podemos definir \(M_L(D_1, f_c, 1)\) y podríamos obtener que, por ejemplo:
\begin{align*} M_L(D_1, f_c, 1) = f_c(D_1) + (N_1, N_2) = (120, 10) + (3, -2) = (123, 8)\\ M_L(D_2, f_c, 1) = f_c(D_2) + (N_1, N_2) = (121, 10) + (-1, 0) = (120, 19) \end{align*}donde los valores \(N_i\) los obtenemos de forma aleatoria con una distribución \(Lap(0,2)\) (en este caso redondeamos a números a enteros para mayor claridad).
Podemos probar rapidamente valores obtenidos de una distribución \(Lap(0,2)\) de la siguiente manera
import scipy.stats dist = scipy.stats.laplace(0, 2) dist.rvs()
Lo primero que podemos observar es el papel que juega el parámetro \(\epsilon\). Al utilizar una distribución \(N_i \sim Lap(0, \Delta f/\epsilon)\) vemos que a medida que aumentamos \(\epsilon\), disminuye el parámetro \(b\) de la distribución. Como se puede observar en la figura 3 cuanto menor es el parámetro \(b\), la distribución de Laplace presenta mayor probabilidad en valores cercanos a \(\mu\), en nuestro caso a 0. Esto quiere decir que cuanto mayor sea \(\epsilon\), menor será \(b\) y por tanto, menor será el ruido añadido.
Uno de los puntos más interesantes sobre este mecanismo de Laplace es que resulta fácil demostrar que satisface \(\epsilon\) -privacidad diferencial. Esto se suele denotar en forma de teorema:
El mecanismo de Laplace satisface \(\epsilon\) -privacidad diferencial.
Si tenemos dos bases de datos vecinas que difieren en un solo elemento \(D_1\), \(D_2\) y el mecanismo de Laplace \(M_L\) para la función \(f\) podemos ver la probabilidad de obtener un mismo resultado \(s\):
\begin{align*} &\frac{P[M_L(D_1, f, \epsilon) = s]}{P[M_L(D_2, f, \epsilon) = s]} = \frac{P[f(D_1) + Lap(0, \frac{\Delta f}{\epsilon}) = s]}{P[f(D_2) + Lap(0, \frac{\Delta f}{\epsilon}) = s]}\\ &= \frac{P[Lap(0, \frac{\Delta f}{\epsilon}) = s - f(D_1)]}{P[Lap(0, \frac{\Delta f}{\epsilon}) = s - f(D_2)]} = \frac{\frac{1}{2b} \exp(-\frac{|s-f(D_1)|}{b})}{\frac{1}{2b} \exp(-\frac{|s-f(D_2)|}{b})}\\ &= \exp \left( \frac{|s - f(D_1)| - |s - f(D_2)|}{b} \right) \leq \exp \left( \frac{|f(D_1) - f(D_2)|}{b} \right)\\ & \leq \exp( \frac{\Delta f}{b} ) = \exp \left( \epsilon \right) \end{align*}4. Continuará…
¿Como podemos aplicar el mecanismo de Laplace en un ejemplo un poco más interesante? ¿Existen otros mecanismos mejores?…
