El mecanismo de Laplace
→ [pdf] ←Sabemos que una manera de proporcionar privacidad diferencial es mediante el uso de un mecanismo aleatorio que puede consistir en añadir ruido a una consulta (o mecanismo) que se realiza a la base de datos.
Ahora veremos un ejemplo de mecanismo aleatorio basado en esta idea conocido como el mecanismo de Laplace. Se trata de uno de los mecanismo más estudiados y sencillos utilizados en privacidad diferencial.
Para introducir este mecanismo veremos que es la sensibilidad de una función, un concepto importante en privacidad diferencial. Esto nos permitirá determinar, en cierta manera, la cantidad de ruido que tenemos que añadir para conseguir un nivel de privacidad determinado a una consulta o función.
Vamos a repasar también, aunque de forma muy rápida, como es una distribución de Laplace, que nos determinará el ruido generado.
1. Distribución de Laplace
La distribución de Laplace (también conocida como doble exponencial) es una distribución de probabilidades continua. Su función de densidad de probabilidad se expresa como:
\[ f(x | \mu, b) = \frac{1}{2b} \exp\left(-\frac{|x - \mu|}{b}\right)\]
donde \(\mu\) es un parámetro de posición o localización y \(b > 0\) un parámetro de escala (o diversidad). Denotaremos esta distribución como \(Lap(\mu, b)\).
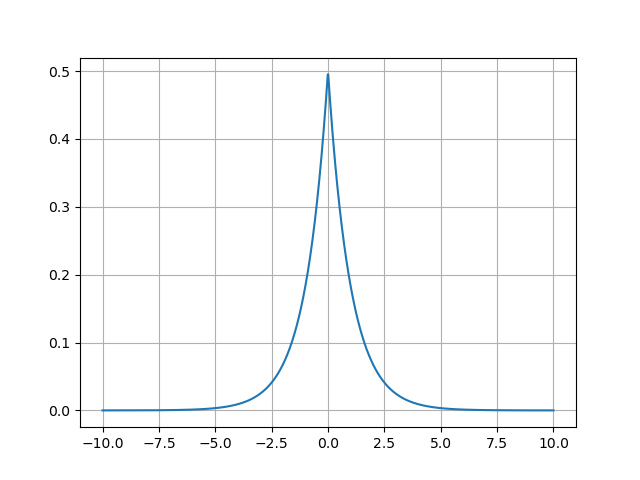
A continuación mostramos la distribución de Laplace \(Lap(0, 1)\), es decir, con \(\mu = 0\) y \(b = 1\).
import scipy.stats import matplotlib.pyplot as plt import numpy as np x = np.linspace(-10,10,1000) dist = scipy.stats.laplace(0, 1) plt.clf() plt.plot(x, dist.pdf(x)) plt.grid() fname = "img/laplace.png" plt.savefig(fname) fname
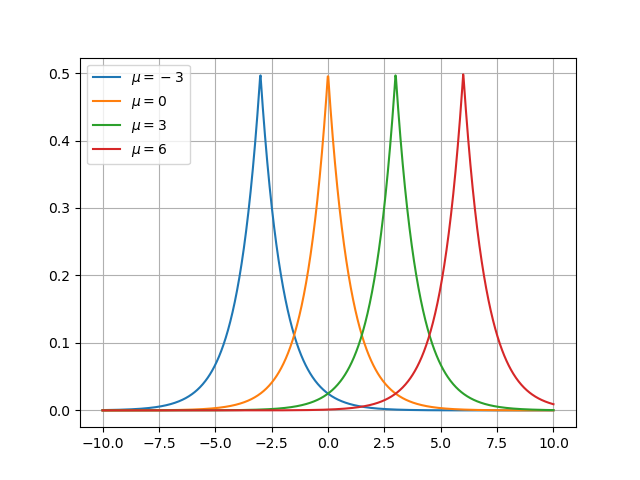
El parámetro \(\mu\) (la media de la distribución) determina la posición o localización de la distribución. Por ejemplo:
plt.clf() for loc in [-3, 0, 3, 6]: dist = scipy.stats.laplace(loc, 1) plt.plot(x, dist.pdf(x), label=f"$\mu = {loc}$") plt.grid() plt.legend() fname = "img/laplace-mu.png" plt.savefig(fname) fname
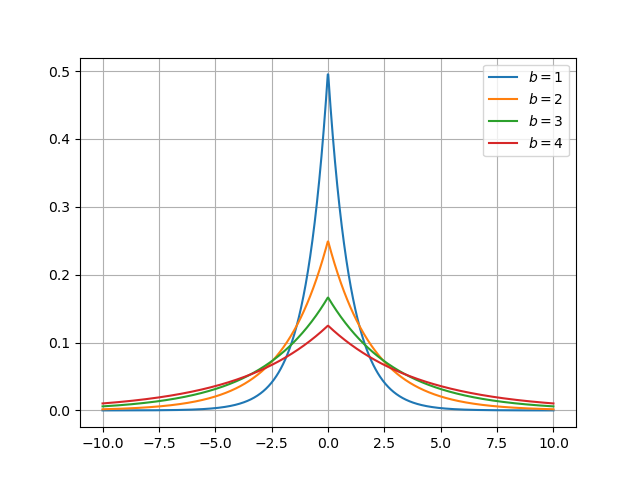
Por otra parte el parámetro \(b\) determina la forma de la distribución (o escala):
plt.clf() for scale in [1, 2, 3, 4]: dist = scipy.stats.laplace(0, scale) plt.plot(x, dist.pdf(x), label=f"$b = {scale}$") plt.grid() plt.legend() fname = "img/laplace-scale.png" plt.savefig(fname) fname
La media de la distribución de Laplace \(Lap(\mu, b)\) es \(\mu\), que coincide con la mediana, y su varianza es \(2b^2\).
2. Sensibilidad global
Consideramos un mecanismo o función \(f\) que realiza una consulta a la base de datos \(D\) generando una respuesta \(f(D)\). Suponemos que los datos a consultar son numéricos y que el resultado puede ser un vector de \(M\) elementos De esta manera, si \(\mathcal{D}\) es el conjunto de todas las posibles bases de datos, \(f: \mathcal{D} \to \mathbb{R}^M\).
La sensibilidad global (global sensitivity) de una funcion \(f\) se suele denotar como \(\Delta f\) o \(GS(f)\), y a veces se llama también \(l_1\) -sensitivity. Queda definida de la siguiente manera:
La sensibilidad global de una función \(f: \mathcal{D} \to \mathbb{R}^M\) es:
\begin{equation} \Delta f = \max_{D_1, D_2 \in \mathcal{D}, d(D_1, D_2) = 1} \lVert f(D_1) - f(D_2) \rVert_{1} \end{equation}En esta definición se utiliza la norma \(l_1\) (\(l_1\) -norm) denotada como \(\lVert \cdot \rVert_1\). Dado un vector \(x \in \mathbb{R}^M\), \(\lVert x \rVert_1 = \sum_{i=1}^M | x_i |\). Podemos ver la norma \(l_1\) simplemente como la suma del valor absoluto de todos los elementos del vector.
Por ejemplo, para el vector \(v = (2, 3, -4, 6)\), su norma \(l_1\) es: \[ \lVert v \rVert_1 = \sum_{i=1}^4 | v_i | = |2| + |3| + |-4| + |6| = 15 \]
La sensibilidad global expresa la máxima diferencia que podemos encontrar al aplicar la función a dos bases de datos que difieren en un solo elemento.
Supongamos que tenemos una base de datos censal con información de la población de nuestra ciudad. Definimos entonces la función \(f_1\) que retorna el número de individuos mayores de edad (con edad mayor o igual a 18).
Tenemos dos versiones de la base de datos que difieren en un solo registro, de manera que, por ejemplo:
\begin{align*} f_1(D_1) = 120\\ f_1(D_2) = 121 \end{align*}en este caso podemos decir que el resultado difiere en 1, pero no es dificil ver que en el caso general la diferencia máxima entre la consulta hecha a dos bases de datos vecinas será 1. Es más, dicha diferencia será siempre -1, 0 ó 1. Podemos entonces decir que la sensivilidad global de \(f_1\) es 1: \[ \Delta f_1 = 1 \]
En general, para cualquier función que consista en contar elementos, como en el ejemplo anterior, tendremos el mismo resultado respecto a su sensivilidad global.
Suponemos ahora que tenemos una segunda funcion \(f_2\) que retorna el número de individuos que han leído el Quijote (información que también incluye la base de datos anterior) y por ejemplo tenemos que:
\begin{align*} f_2(D_1) = 10\\ f_2(D_2) = 10 \end{align*}Al igual que con \(f_1\) es fácil ver que \(\Delta f_2 = 1\).
Vamos ahora a ver la función \(f_c\) que definimos como aquella que retorna un vector con las dos consultas correspondientes a \(f_1\) y \(f_2\), de manera que \(f_c(D) = (f_1(D), f_2(D))\). Siguiendo el ejemplo anterior podríamos tener:
\begin{align*} f_c(D_1) = (120, 10)\\ f_c(D_2) = (121, 10) \end{align*}En este caso la sensibilidad global será de 2. La diferencia máxima para cada función es 1, con lo que la norma \(l_1\) será 2. Es decir \(\Delta f_c = 2\)
El lector obviamente se preguntará que pasa en el caso de funciones más complejas e interesantes. Aquí es donde se puede complicar un poco el asunto ya que podríamos tener funciones para las que su sensibilidad global sea infinito o resulte difícil poder estimar un cálculo. En general necesitaremos que la función este acotada para poder calcular su sensibilidad global. Queda pendiente ver con mayor detalle casos diferentes a funciones que cuenten registros.
3. El mecanismo de Laplace
Llegamos ya a poder ver uno de los mecanismos aleatorios más populares en privacidad diferencial, el conocido como mecanismo de Laplace. Sin muchas sorpresas, éste consiste en añadir ruido siguiendo una distribución de Laplace a la respuesta.
Consideramos una consulta o mecanismo \(f\) que realiza una consulta a la base de datos \(D\) generando una respuesta \(f(D)\). A modo de generalización suponemos que los datos a consultar son numéricos y la respuesta, un vector de \(M\) elementos. De esta manera, si \(\mathcal{D}\) es el conjunto de todas las posibles bases de datos, \(f: \mathcal{D} \to \mathbb{R}^M\).
El mecanismo de Laplace para la función \(f\mathcal{D} \to \mathbb{R}^M\) es:
\begin{equation*} M_L(D, f, \epsilon) = f(D) + (N_1, \ldots, N_M) \end{equation*}donde \(D \in \mathcal{D}\), y \(N_i\) son variables aleatorias independientes que se obtienen a partir de una distribución de Laplace \(N_i \sim Lap(0, \Delta f/\epsilon)\).
Siguiendo el ejemplo anterior podemos definir \(M_L(D_1, f_c, 1)\) y podríamos obtener que, por ejemplo:
\begin{align*} M_L(D_1, f_c, 1) = f_c(D_1) + (N_1, N_2) = (120, 10) + (3, -2) = (123, 8)\\ M_L(D_2, f_c, 1) = f_c(D_2) + (N_1, N_2) = (121, 10) + (-1, 0) = (120, 19) \end{align*}donde los valores \(N_i\) los obtenemos de forma aleatoria con una distribución \(Lap(0,2)\) (en este caso redondeamos a números a enteros para mayor claridad).
Podemos probar rapidamente valores obtenidos de una distribución \(Lap(0,2)\) de la siguiente manera
import scipy.stats dist = scipy.stats.laplace(0, 2) dist.rvs()
Lo primero que podemos observar es el papel que juega el parámetro \(\epsilon\). Al utilizar una distribución \(N_i \sim Lap(0, \Delta f/\epsilon)\) vemos que a medida que aumentamos \(\epsilon\), disminuye el parámetro \(b\) de la distribución. Como se puede observar en la figura 3 cuanto menor es el parámetro \(b\), la distribución de Laplace presenta mayor probabilidad en valores cercanos a \(\mu\), en nuestro caso a 0. Esto quiere decir que cuanto mayor sea \(\epsilon\), menor será \(b\) y por tanto, menor será el ruido añadido.
Uno de los puntos más interesantes sobre este mecanismo de Laplace es que resulta fácil demostrar que satisface \(\epsilon\) -privacidad diferencial. Esto se suele denotar en forma de teorema:
El mecanismo de Laplace satisface \(\epsilon\) -privacidad diferencial.
Si tenemos dos bases de datos vecinas que difieren en un solo elemento \(D_1\), \(D_2\) y el mecanismo de Laplace \(M_L\) para la función \(f\) podemos ver la probabilidad de obtener un mismo resultado \(s\):
\begin{align*} &\frac{P[M_L(D_1, f, \epsilon) = s]}{P[M_L(D_2, f, \epsilon) = s]} = \frac{P[f(D_1) + Lap(0, \frac{\Delta f}{\epsilon}) = s]}{P[f(D_2) + Lap(0, \frac{\Delta f}{\epsilon}) = s]}\\ &= \frac{P[Lap(0, \frac{\Delta f}{\epsilon}) = s - f(D_1)]}{P[Lap(0, \frac{\Delta f}{\epsilon}) = s - f(D_2)]} = \frac{\frac{1}{2b} \exp(-\frac{|s-f(D_1)|}{b})}{\frac{1}{2b} \exp(-\frac{|s-f(D_2)|}{b})}\\ &= \exp \left( \frac{|s - f(D_1)| - |s - f(D_2)|}{b} \right) \leq \exp \left( \frac{|f(D_1) - f(D_2)|}{b} \right)\\ & \leq \exp( \frac{\Delta f}{b} ) = \exp \left( \epsilon \right) \end{align*}4. Continuará…
¿Como podemos aplicar el mecanismo de Laplace en un ejemplo un poco más interesante? ¿Existen otros mecanismos mejores?…
