Respuesta aleatoria (randomized response)
→ [pdf] ←La respuesta aleatoria, en inglés randomized response, o simplemente RR es una técnica introducida en [1] que permite realizar encuestas sobre preguntas sensibles manteniendo cierto nivel de privacidad de las personas que contestan. Como veremos el uso de esta técnica se ha visto popularizado precisamente por sus aplicaciones en privacidad diferencial.
1. Respuesta aleatoria con una moneda
Un ejemplo sencillo de respuesta aleatoria se suele ejemplificar con el lanzamiento de una moneda. Supongamos que queremos hacer una pregunta sensible a un grupo de personas. Por ejemplo: ¿ha consumido drogas en el último mes? Se trata de una pregunta cuya respuesta será "SI" o "NO".
Para responder la pregunta pedimos a las personas encuestadas que sigan el proceso descrito a continuación:
- Lanzar una moneda (en secreto, sin que nadie vea el resultado):
- si sale cara: decimos la verdad
- si sale cruz: decimos que SI
Únicamente la persona que contesta sabe si ha salido cara o cruz. Nosotros, que recogemos las respuestas, no sabemos si una respuesta afirmativa es fruto de que ha salido cruz o realmente refleja la verdad (la persona encuestada puede negar que una respuesta "SI" sea cierta). En este sentido decimos que el método proporciona strong deniability para cualquier respuesta "SI". Cabe notar que en el caso de una respuesta "NO", sí que sabemos que la respuesta es verdadera.
La gracia de este método es que si tenemos un número de respuestas elevado podemos estimar con cierta exactitud el numero de personas que han consumido drogas. Esto es porque podemos asumir que la probabilidad de que salga cara es de \(1/2\) y por tanto en la mitad de las respuestas habrá salido cara y en la otra mitad cruz. Cuantas más respuestas tengamos, más exacta será esta asunción.
Es decir, si tenemos \(100\) respuestas:
- en \(50\) de ellas habrá salido cruz i por tanto su respuesta sera SI,
- en \(50\) de ellas habrá salido cara i por tanto su respuesta será la verdad. Supongamos que en \(30\) de ellas la respuesta es "NO", y por tanto en \(50 - 30 = 20\) la respuesta es "SI".
Ahora asumimos que la distribución de respuestas entre los encuestados a los que les ha salido cara y cruz es la misma. Es decir habrá aproximadamente el mismo numero de encuestados que han consumido drogas entre los que han obtenido cara y los que han obtenido cruz.
De esta manera entre los 50 que les ha salido cara tendremos también \(30\) que no han consumido drogas. Lo que nos da un total de \(60\) encuestados que NO han consumido drogas del total de \(100\) (y en consecuencia, \(40\) sí que han consumido drogas).
Es importante remarcar que esta conclusión se obtiene únicamente observando el número de respuestas "NO". Si el numero de respuestas obtenidas "NO" es de \(p\), el total de respuestas reales "NO" será de \(2p\).
2. Respuesta aleatoria y privacidad diferencial
Para ver la relación entre privacidad diferencial y RR vamos a complicar un poco el proceso descrito anteriormente. El planteamiento es el mismo: ¿Ha consumido drogas en el ultimo mes?, con posible respuesta SI o NO. Sin embargo ahora definimos el proceso de respuesta de la siguiente manera:
- Lanzamos una moneda
- Si sale cara: decimos la verdad
- Si sale cruz: volvemos a lanzar la moneda:
- Si sale cara: decimos SI
- Si sale cruz: decimos NO
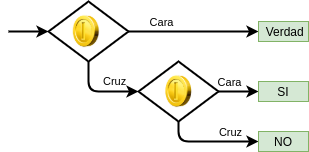
Podemos ver el diagrama de flujo correspondiente en la figura 1. En este caso lanzamos también la moneda, con cara respondemos de forma sincera, y si obtenemos cruz volvemos a lanzar la moneda y respondemos "SI" si sale cara o "NO" si sale cruz.
En este caso, a diferencia del anterior, tanto la respuesta "SI" como "NO" proporciona strong deniability. No sabemos si la persona encuestada esta diciendo la verdad o no en ambos casos.
En la siguiente Tabla podemos ver cada caso desglosado según salga cara o cruz en los lanzamientos de moneda. La primera columna muestra la respuesta verdadera mientras que la columna Respuesta muestra la respuesta que dará la persona encuestada al utilizar este esquema de RR dependiendo de los resultado de tirar la moneda. En la última columna podemos ver la probabilidad de cada caso.
| Verdad | 1a Moneda | 2a Moneda | Respuesta | Probabilidad |
|---|---|---|---|---|
| SI | Cara | - | SI | 0.5 |
| SI | Cruz | Cara | SI | 0.25 |
| SI | Cruz | Cruz | NO | 0.25 |
| NO | Cara | - | NO | 0.5 |
| NO | Cruz | Cara | SI | 0.25 |
| NO | Cruz | Cruz | NO | 0.25 |
Si denotamos como \(P[Resp=SI \mid Verdad=SI]\) la probabilidad de obtener una respuesta "SI" cuando la verdad es "SI", tenemos las probabilidades siguientes:
| \(P[Resp=SI \mid Verdad=SI] = 0.75\) |
| \(P[Resp=SI \mid Verdad=NO] = 0.25\) |
| \(P[Resp=NO \mid Verdad=SI] = 0.25\) |
| \(P[Resp=NO \mid Verdad=NO] = 0.75\) |
donde podemos ver que:
\begin{equation} \frac{P[Resp=SI \mid Verdad=SI]}{P[Resp=SI \mid Verdad=NO]} = \frac{P[Resp=NO \mid Verdad=NO]}{P[Resp=NO \mid Verdad=SI]} = \frac{0.75}{0.25} = 3 \end{equation}por lo que se dice que esta versión de RR cumple privacidad diferencial para \(\epsilon = \ln 3\) [2].
Con esta versión de RR también podemos estimar el número de personas que han consumido drogras a partir de las respuestas obtenidas. En este caso supongamos que \(Y\) es el número de respuestas "SI" recibidas, y asumimos que \(p\) es la proporción real (verdadera) de personas que sí que se han drogado. De esta manera tenemos que:
\begin{equation} Y = \frac{3}{4} p + \frac{1}{4} (1 - p) = \frac{1}{4} + 2 p \end{equation}Del total de personas encuestadas, responderan "SI" \(3/4\) de las que sí que se han drogado (\(p\)), y \(1/4\) de las que no se han drogado (\(1 - p\)). De manera que \(p = 2Y - \frac{1}{2}\).
